Keith L. Dougherty, Political Science, American Politics




	Incomplete Information Game: US and Soviet Payoffs Unknown

	What follows is a symmetric representation of the Cuban Missile Crisis game where both sides have incomplete information (i.e. don't know the other side's payoffs; they only know what they could be). Here q is the probability that the US is a hardliner; (1-q) is the probability that the US is soft; p is the probability that the USSR is a hardliner, (1-p) is the probability that the USSR is soft. Furthermore, the actions are labeled with letters (t = threaten, n = not threaten, w = withdraw, and d = defy). In addition, there are four information sets. For the US, decision nodes US.1 and US.2 are in the same information set and US.3 and US.4 are in another information set. For the USSR, decision nodes USSR.1 and USSR.3 are in a third information set and USSR.2 and USSR.4 are in a fourth information set. These are indicated by the dotted lines. The sequential equlibrium is found using a combination of expected value and backward induction. We start by considering each of the information sets for the soviets (because they move last) then each of the information sets for the Americans. 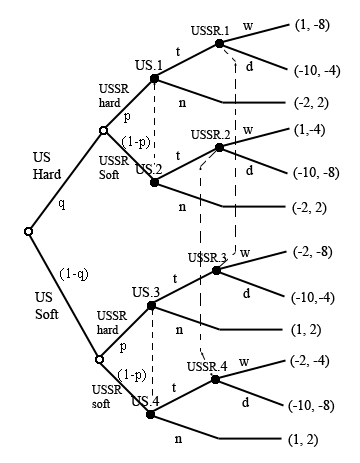USSR Hard (info set = {USSR.1, USSR.3}) Expected Payoff to Soviets for withdraw: qp(-8) + (1-q)p(-8) = p(-8q - 8 + 8q) = p(-8). Expected Payoff to Soviets for defy: qp(-4) + (1-q)p(-4) = p(-4q - 4 + 4q) = p(-4). Therefore, soviets always defy at this information set because -4p > -8p (...since 0 <= p <= 1). Note: you can ignore the p's here because the Soviets know they are hard. I left them in so that you would not get confused. USSR Soft (info set = {USSR.2, USSR.4}) Expected Payoff to Soviets for withdraw: q(1-p)(-4) + (1-q)(1-p)(-4) = (1-p)(-4q -4 + 4q) = (1-p)-4. Expected Payoff to Soviets for defy: q(1-p)(-8) + (1-q)(1-p)(-8) = (1-p)(-8q -8 + 8q) = (1-p)-8. Therefore, soviets always withdraw at this information set because -4(1-p) > -8(1-p). US Hard (info set = {US.1, US.2}) Expected Payoff to Americans for threaten: qp(-10) + q(1-p)1 = q(-10p + 1 - p) = q(-11p + 1). Expected Payoff to Americans for not: qp(-2) + q(1-p)-2 = q(-2p - 2 + 2p) = q(-2). Therefore, Americans threaten at this information set if and only if. q(-11p + 1) > q(-2) = -11p > -3 = p < 3/11 Note: the Americans threaten depending upon p, similar to what we discussed in class. US Soft (info set = {US.3, US.4}) Expected Payoff to Americans for threaten: (1-q)p(-10) + (1-q)(1-p)-2 = (1-q)(-10p - 2 + 2p) = (1-q)(-8p - 2). Expected Payoff to Americans for not: (1-q)p1 + (1-q)(1-p)1 = (1-q)(p + 1 - p) = (1-q)1. Therefore, Americans threaten at this information set if and only if. (1-q)(-8p - 2) > (1-q)1 = -8p - 2 > 1 = -8p > 3 = p < -3/8 which is never the case. Hence, the Americans will never threaten at this information node. In other words, if the Americans are soft, they back down. The Sequential Equlibrium is conditioned on player type and can be written: {([not \| soft], [threaten \| p < 3/11]); ([defy \| hard], [withdraw \| soft])}. Note: everything before the ";" is the strategy of the US. Everything after is the strategy for the USSR.
Last Modified: 6/17/08

Keith L. Dougherty | Department of Political Science | University of Georgia